The Tower of Hanoi

Concrete Mathematics begins with the well-known — at least among the teachers and students of computer science and programming — a neat little puzzle Tower of Hanoi. And it is cool since I hope the text would finalize curing me of an aversion I used to feel towards this puzzle (and a couple of others 🤐). But before that, I'd like to think over the puzzle solution myself.

For that, let's imagine we're children 🧒👧👦. Our mommies and daddies gave us a game to play: three sticks on the stands and a bunch of disks, each of a different size. How nice of them indeed 🤨.

The goal of this game is to move a "tower" — a group of disks ordered from the largest to the smallest bottom to top — from the initial stick (A) to another stick (Z) one by one. There's a restrictive rule in this game: it is forbidden to put a large disk atop a smaller one. Any stick can be utilized along the way as long as the restrictive rule is not broken. And — since we're just imagining that we're playful children, in reality trying to compute something — we're going to count the least number of moves we have to make.

First, we imagine being really small children 👶. Not to spook us away, we are given only a few disks. We joyfully launch those disks for a flight from one stick to another:

One disk

We just move it from the stick A to the stick Z. Boom! Done!
This is just 1 move.

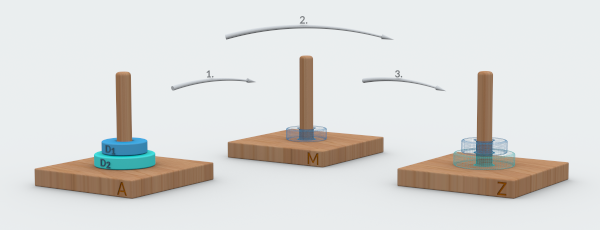
Two disks

1. Move disk D₁ to the stick M.
2. Move disk D₂ to the final destination: stick Z.
3. Move disk D₁ to the stick Z.
In total, 3 moves.

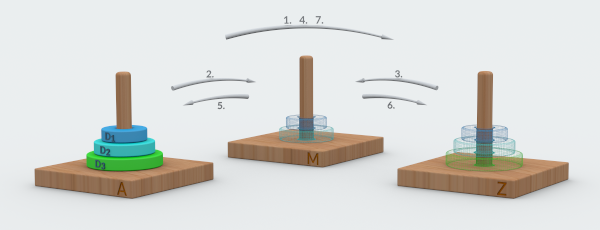
Three disks

1. Disk D₁ to Z.
2. Disk D₂ to M.
3. Disk D₁ to M (atop the disk D₂).
4. Disk D₃ goes to the final stick Z and rests there.
5. Disk D₁ moves back to A.
6. Disk D₂ to Z.
7. Disk D₁ to Z too.
In total, 7 moves.

Now stop and think. Translocating those disks around in our imagination (or doing it in reality, even with the pieces of paper, if it's difficult to play imaginary games yet), try to find any patterns: repeated moves for instance. Try to find a criterion to break up scattered moves of random disks into groups.

Pause… Think… Breath…

Well, I'll try to formulate what I have found playing this imaginary game.

After moving a tower consisting of one disk to the final position (1 move), we had learned how to solve the puzzle for one disk. This means, that from now on, whenever a one-disk tower will have to be moved, we'd know how to do it and how many moves it would require. Of course, a one-disk tower requiring just one move is trivial knowledge by itself. But we're going to base more and more complex understanding by combining pieces of triviality. Isn't it what math and programming are about? 😉

Now consider the tower built of two disks. First, we need to open up a way for the larger disk. And that we can do by moving the smaller disk (a one-disk tower) to the helper stick M (1 move as we already know). Then we need to move the larger disk (a one-disk tower) to the final position on the stick Z (1 move again). And then we need to move a tower consisting of the smaller disk to the stick Z too (1 move once again).

The same is for the 3 disks tower. We already know that we need 3 moves to relocate the smaller two disks (a.k.a. a two-disks tower). And we need to do it twice: the first time to open a way for the largest disk; the second time to move them to the final position. And in between, we make 1 move with the largest disk: from the stick A to the stick Z.

To summarize, we had identified the following types of moves:

1. Open the way for the largest disk by moving the rest of the tower to the stick M.
2. Move the largest disk to the stick Z.
3. Move the rest of the tower atop the largest disk on the stick Z.

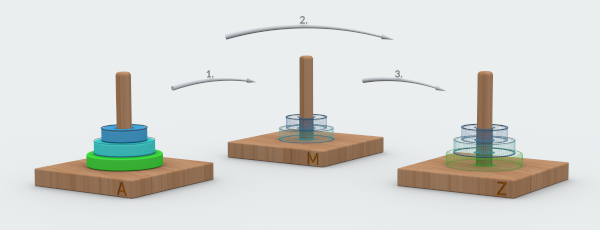
And they can be combined into just two groups:

• Move the largest disk.
• Move the rest of the tower twice.

Let's pause here, contemplating the beauty of the pattern…

Next step. Look at the numbers we have. For clarity, the following table lists cases up to the 8-disks tower.

Number of Disks	Number of Moves Grouped	Number of Moves
1	0 + 1 + 0	1
2	1 + 1 + 1	3
3	3 + 1 + 3	7
4	7 + 1 + 7	15
5	15 + 1 + 15	31
6	31 + 1 + 31	63
7	63 + 1 + 63	127
8	127 + 1 + 127	255

Do the numbers in the last column remind you of something? Try to find a pattern, and then a formula to calculate a number of moves given the number of disks.

Pause… Think… Breath…

A tip: now I understand why all the programming/computer science instructors seem to adore this puzzle.

Pause… Think… Verify.

Yeah, those are the powers of two minus one.

Hence, a tower of 64 disks should require an impressive number of 18446744073709551616 moves (if my calculator didn't lie of course).

Well, now, after resolving the years-long aversion to The Tower of Hanoi puzzle (what a Gestalt it was!), and after hacking into its internals by myself, I'm ready to continue reading the book and comprehending whatever the authors have to tell about it.